ВОЗМОЖНОСТИ КОМПЬЮТЕРНОЙ РЕСТАВРАЦИИ
Очень часто археологические находки попадают к археологам в разрушенном или даже руинированном виде. Многие из них попадают в культурный слой уже в сломанном состоянии — расколовшись на обломки, части которых может не быть вообще, к тому же, предметы могут деформироваться, теряя свой первоначальную геометрию.
Решение задачи компьютерного моделирования процесса реставрации археологических находок и, хотя бы частичная автоматизация скрупулезной работы с материалом раскопок, которой терпеливо занимаются реставраторы, является актуальным направлением автоматизации археологических изысканий.
При разработке методики реставрации геометрической формы предметов, нашей конечной целью являлось построение математических моделей геометрии этих объектов. Эти модели должны помочь реставратору при проведении исследований, в основном, для принятия решений на основе предварительной компьютерной визуализации, а также дают возможность выполнить исследование многих физических свойств объекта путем постановки численных экспериментов.
Активная разработка технологии длилась около года, за которые было отснято и изучено множество образцов разной степени целостности и проведение анализа с целью нахождения закономерностей геометрии и приведения их в форму математических зависимостей. Однако, тут используется уже более совершенный алгоритм. Повышена точность и устранены ошибки геометрии. Также включены еще два контура проверки адекватности.
В качестве примера принципа действия технологии, рассмотрим керамический сосуд с частично утерянными элементами, составляющими 57% объема материала сосуда. Кроме того, что это очень большой процент утерь, сложностью данного процесса реставрации является то, что основной процент потерь приходится на единую область, а не разбит на множество мелких, реставрация которых очевидна и не вызывает больших погрешностей.

Для задания процесса компьютерного реставрирования, необходимо выработать определенную логику, согласно которой и будет происходить сам процесс. Конечно, учитывая, что керамический сосуд является чисто ручной работой и его геометрия слабо ограничена какой-то технологией, кажется, что точно восстановить такую большую область невозможно. Потому что, теоретически, утерянная часть сосуда может представлять собой что угодно или варьироваться в пределах, которые не позволят утверждать, что процесс реставрации восстанавливает действительную форму сосуда.
Реставратор, проводя данную работу исходит из своего опыта, который базируется, однако, не только на большом количестве виденного им материала и на понимании самого процесса изготовления, но, зачастую и на представлении, каким должно бы быть изделие в гипотетически идеальном случае с учетом технологии и качества работы данного мастера. То есть, понимать задумку автора и учитывать его реальные возможности.
Именно последнее утверждение можно использовать для компьютерного способа реставрации, который нуждается в четко поставленной задаче и четкой логике исполнения.
Ведь, задача реставрации утерянных частиц сосуда, в конечном итоге, является задачей построения поверхности, имеющей определенные радиусы кривизны в каждой ее точке или ограниченном сегменте.
Проанализируем вначале форму сосуда для определения максимальных допусков, уже существующих в геометрии. Анализ будем проводить с помощью продольных и поперечных сечений, проходящих в заданных местах, таким образом, чтобы эти сечения, соединяясь кривыми, наиболее полно повторяли форму сосуда, в результате получая единую трехмерную форму. Данный процесс построения поверхности по ее сечениям, по сути, является плазированием, применяемым для построения сложных математически не описываемых сплайновых поверхностей.
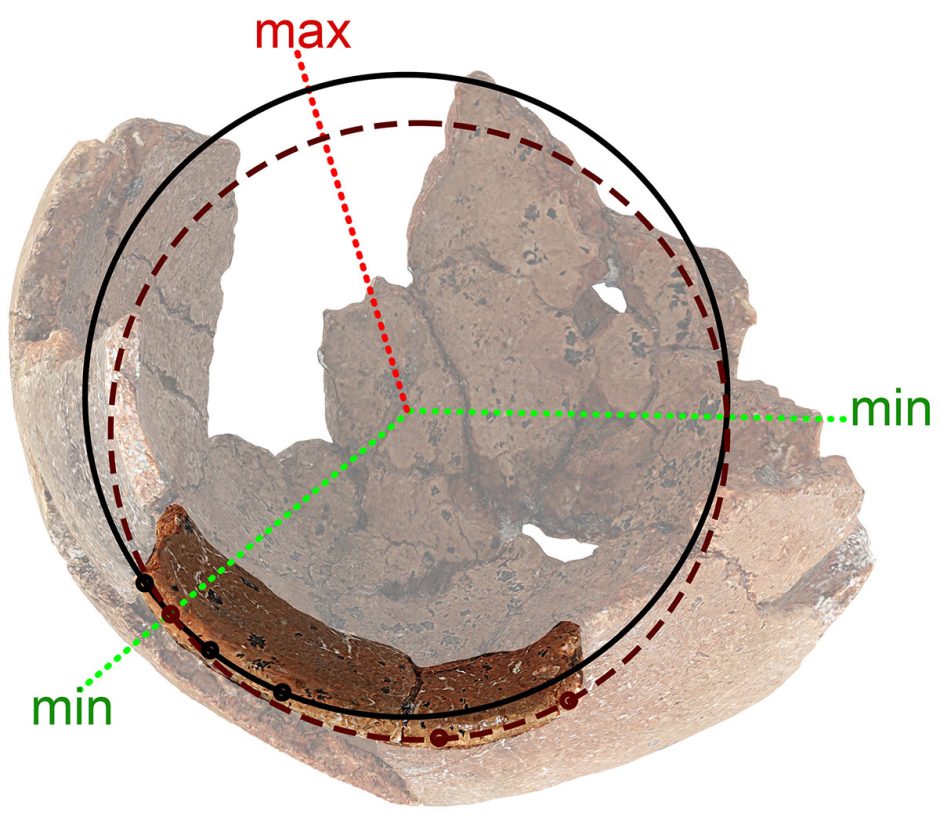
Определение того самого «мастерства» изготовителя и возможностей его технологии, с точки зрения геометрических выкладок сводится к определению погрешности от той геометрии, которую хотел достичь мастер.
Анализ данных сечений показывает, что отклонение от круглости не превышает 8%. Однако, такая большая погрешность существует только в одном сечении сосуда и, скорее всего, связана с неправильно произведенной склейкой деталей. В остальных же сечениях, отклонение от круглости не превышает 6%.
И становится очевидно, что, хотя, да, конечно, сосуд не является телом вращения и не изготовлен на гончарном круге, но изготовитель явно стремился к тому, чтобы сделать его «ровным», то есть достичь геометрии тела вращения. Будем считать это пределом расчётов с учетом погрешностей мастерства и технологии, заложенных в геометрии данного сосуда.
На рисунке видно смещение сосуда от осей симметрии, что выглядит странно, но является, как ни странно, единственными вариантами с сохранением критериев радиусов и точек сопряжения кривых. Это может быть связано, конечно, как с кривизной реально существующего сосуда, так и погрешностью склейки частей реставратором.
Кстати, проведение именно подобного анализа может показать данный факт. При непосредственно склейке, глазом это не видно.
Учитывая эту информацию и предполагая, что в потерянной геометрии сосуда эта закономерность явно сохранится, мы можем построить некий коридор максимумов и минимумов координат для каждой точки сосуда и после определить главные кривизны поверхности, которые являются максимальной и минимальной кривизнами соответственно.
Для того чтобы начать наши построения, нам необходимо сначала построить некое облако точек, на основании которого мы сможем построить поверхность и ответить на вопрос, принадлежит ли точка области условной поверхности сосуда с учетом определенных погрешностей.
Для того чтобы установить принадлежность точки некоторой двухмерной поверхности, необходимо найти все точки, принадлежащие всем сечениям с условием их пересечения с границами области.
Результатом явилось облако точек, в пределах которого теоретически может находиться геометрия сосуда.
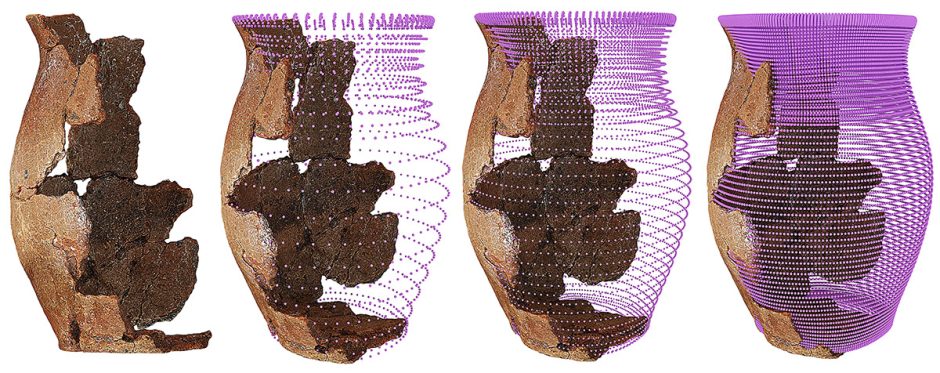
Данное облако точек весьма неоднозначно определит поверхность. Такую область изменения параметров могут иметь очень многие поверхности, и для построения недостающей части сложной формы необходимы предварительные построения упрощающие дальнейший процесс. Для нас практическое значение будут иметь пространственные линии, как и точки, лежащие в области заданных параметров.
Для последующего построения поверхности можно построить два семейства ортогональных в точке их пересечения кривых при различных значениях критериев – максимума и минимума. Два таких семейства кривых образуют сетку.
Через каждую точку можно провести множество различных кривых, и величина их достоверности будет иметь одно и то же значение, несмотря на то, что у них разная кривизна. Единственным критерием отбора здесь может являться лишь то, что кривизна такой кривой должна быть в интервале кривизны, определяемым максимумом и минимумом нормального сечения в данной точке
Для своей работы мы использовали NURBS-кривые.

Пусть мы начертили некоторую кривую, соединив для этого ряд точек. При этом, кривизна этой линии будет меняться в зависимости от того, какие именно точки мы использовали для создания опорных для данной кривой. На построенном нами облаке точек можно построить огромное количество подобных кривых, из которых необходимо выбрать адекватные.
За определение главных критериев для кривых можно принять следующее: адекватными можно считать кривые, для которых кривизна нормального сечения принимает максимальное и минимальное значение в заданном выше диапазоне.
Так как функции построения подобных кривых не являются независимыми, и они связаны между собой уравнениями, то семейств кривых, полностью удовлетворяющих условиям где следующая точка линии не должна выйти за сферу смещения, будет не так много. И отбор кривых с максимальной степенью адекватности не представляет труда даже в ручном режиме. Что предпочтительнее, так как компьютер все-таки не может полностью заменить человека в области нечеткой логики и может лишь выдать ему на рассмотрение все возможные траектории.
Построение математической модели поверхности происходит аналогично построению кривых. Мы ограничиваем функции поверхности некоторыми значениями ее параметров и получаем геометрическую информацию о поверхности в точке, соответствующей данным значениям параметров.
После построения геометрии поверхности сосуда, полученная поверхность текстурировалась для придания более реалистичного внешнего вида уже вручную, методом плавного заполнения выбранной части изображения содержимым, сходным со смежными участками текстуры.
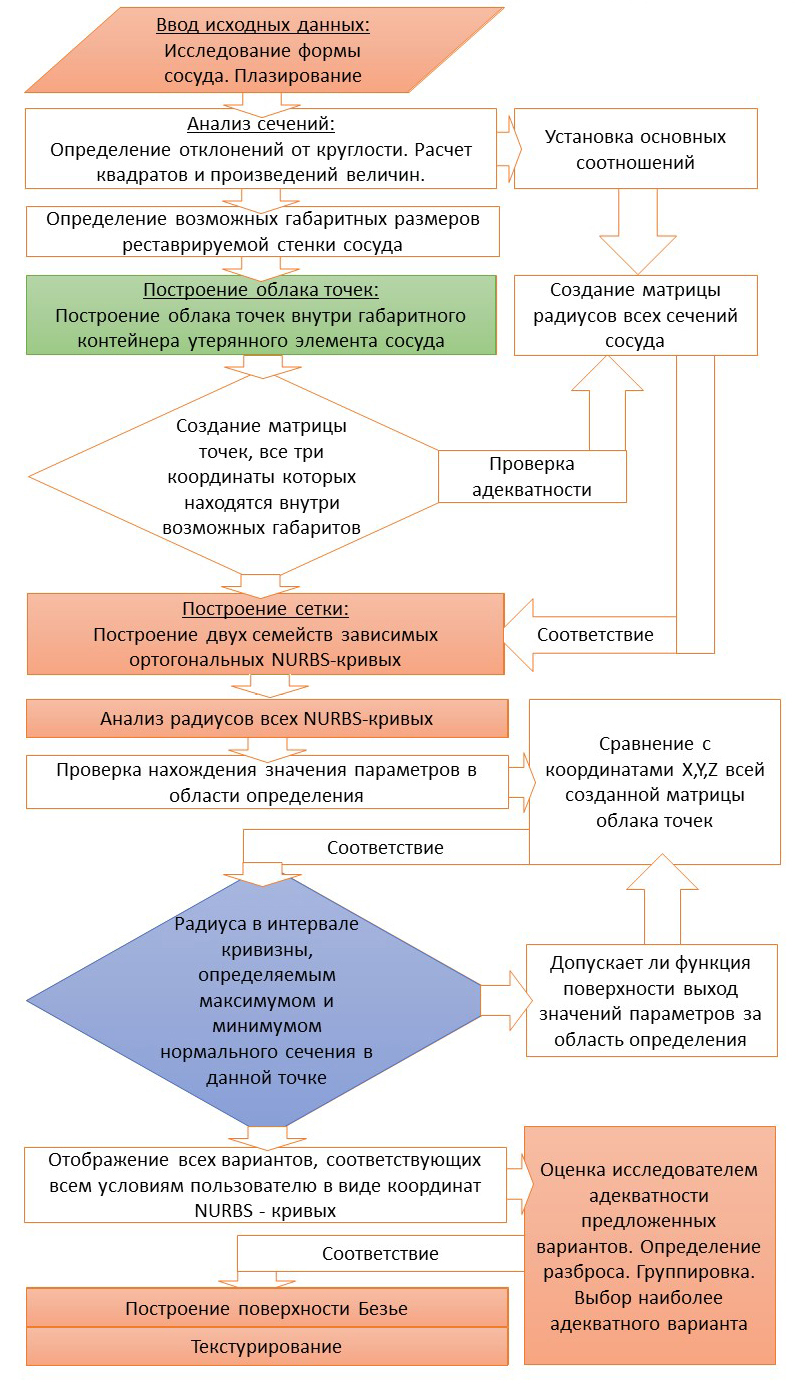
Логическую схему процесса реставрации можно представить в виде блок-схемы:
Конечный результат отражает полный возможный внешний вид сосуда:

После проведения компьютерной реставрации, восстанавливающей наиболее вероятную форму сосуда можно сделать ортогональные виды, сделать сечения.

А также узнать возможные размеры сосуда:
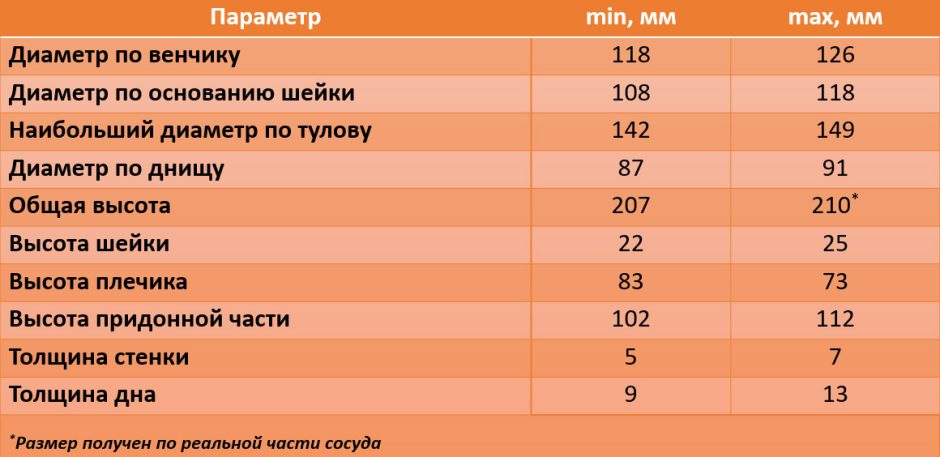
Хочется отметить, что компьютерное моделирование по данному алгоритму не дает единственного варианта формы сосуда, однако, набор предлагаемых форм отличается не так сильно. Максимальное отклонение вариантов обычно варьируется в пределах ±6мм. Это различие представляет интерес для непосредственной работы с 3D-моделью и дальнейшего исследования характеристик сосуда, но несущественно для визуализации.
ВЫВОДЫ
В настоящее время предложена технология реставрации объектов, близких к объектам вращения. Для реставрации достаточно иметь небольшой участок реального объекта с хорошо определяемым радиусом кривизны. Чем меньше участок и чем ближе точки на дуге, тем будет больше вариантов реставрируемых форм и тем более они будут отличаться друг от друга.
И, хотя, конечно, мы понимаем, что реставрация не более, чем вариант предсказания и определения наиболее вероятной, а не реальной формы, данная технология может помочь исследователю в реставрировании и, главное, в оценке адекватности и геометрической правильности реставрированных им изделий. Что особенно актуально при утрате большого объема объекта реставрации, когда реставратору не видна полная геометрия объекта.
Предлагаемый метод по существу является частным случаем метода математического моделирования, цель которого — не заменить опыт специалиста, а дать в его распоряжение инструмент, позволяющий более глубоко вникнуть в суть исследованных явлений.